La fractale de Mandelbrot – Codage en Python

Quel est le point commun entre un chou romanesco, les côtes terrestres, une feuille de fougère ou bien encore un flocon de neige ? Tous ces éléments sont de nature fractale, c’est-à-dire qu’il possède une propriété d’auto-similarité quelle que soit l’échelle à laquelle on les observe. Autrement dit, le tout est semblable à l’une de ses parties. C’est en reprenant les travaux de Gaston Julia et Pierre Fatou que Benoît Mandelbrot a introduit et définit le terme « fractale ». Grâce aux moyens informatiques dont il disposait, il a pu obtenir une représentation « visuelle » de ces objets mathématiques que ces prédécesseurs ne pouvaient seulement qu’imaginer.

Dans cet article, nous allons définir l’ensemble de Mandelbrot, écrire un algorithme permettant de déterminer si un point du plan fait partie ou non de cet ensemble et enfin écrire un programme Python permettant de visualiser la fractale de Mandelbrot.

Un ensemble de ressources sur la programmation Python pour la spécialité NSI est disponible afin d’en maîtriser les espects fondamentaux.

I – Définition de la fractale de Mandelbrot

Soit un point donné \( C(c_x;c_y) \) du plan muni d’un repère \( (O;\vec{u},\vec{v}) \) . Pour tout entier naturel \( n \), on construit, à partir des coordonnées de ce point \( C \),  une suite de points \( M_n(x_n;y_n) \) défini par les relations de récurrence suivantes :

\( \left\lbrace\begin{array}{l} x_0=y_0=0\\ x_{n+1}=x_n^2-y_n^2 +c_x\\ y_{n+1}= 2x_ny_n+c_y\end{array}\right. \)

Pour déterminer si le point \( C \) appartient ou non à l’ensemble de Mandelbrot, on commence par calculer quelques termes des suites \( (x_n) \) et \( (y_n) \). Prenons deux exemples concrets (en arrondissant les résultats) :

• Soit \( C(1;1) \), alors la suite des points \( (M_n) \) construite à partir de ce point \( C \) est \( M_0(0;0) \) ;  \( M_1(1;1) \) ; \( M_2(1;3) \) ; \( M_3(-7;7) \) ; \( M_4(1;-97) \) ; \( M_5(-9407;-193) \)
• Soit \( C(0,1;0,2) \), alors la suite des points \( (M_n) \) construite à partir de ce point \( C \) est \( M_0(0;0) \) ;  \( M_1(0,1;0,2) \) ; \( M_2(0,07;0,24) \) ; \( M_3(0,0473;0,234) \) ; \( M_4(0,0477;0,222) \) ; \( M_5(0,0529;0,221) \)

Nous allons nous intéresser à la distance \( OM_n = \sqrt{x_n^2+y_n^2} \) c’est-à-dire à la distance qui sépare le point \( M_n \) de l’origine du repère et nous pouvons constater que deux cas de figures peuvent se présenter :

• Soit la distance \( OM_n \) augmente infiniment, autrement dit les suites \( (x_n) \) et \( (y_n) \) divergent vers l’infini.
• Soit la distance \( OM_n \) est bornée, autrement dit les suites \( (x_n) \) et \( (y_n) \) sont bornées.

Evidemment, tout ceci n’est que conjecture puisque nous n’avons calculer que les 6 premiers termes de chaque suite. Toutefois, un résultat que l’on admettra permet d’affirmer que si la distance \( OM_n \) devient supérieure à 2 à partir d’un certain rang, alors les suites divergent et la distance \( OM_n \) tend vers l’infini. En revanche, si pour une certaine valeur de \( n \) suffisamment grande, la distance \( OM_n \) reste inférieure à 2, alors on pourra considérer que les deux suites sont bornées et que cette distance \( OM_n \) est bornée (minorée par 0 et majorée par 2).

La règle de prise de décision quant à l’appartenance du point \( C(c_x;c_y) \) à l’ensemble de Mandelbrot est alors la suivante :

• Soit le point \( M_n \) « s’éloigne » infiniment de l’origine auquel cas le point \( C \) n’appartient pas à l’ensemble de Mandelbrot, ce qui est le cas du point \( C \) de coordonnées \( (1;1) \)
• Soit le point \( M_n \) « reste » au voisinage de l’origine c’est-à-dire dans un cercle de centre O et de rayon 2, auquel cas le point \( C \) appartient à l’ensemble de Mandelbrot, c’est le cas du point \( C \) de coordonnées \( (0,1;0,2) \)

II – La fractale de Mandelbrot en Python

Maintenant que nous pouvons dire si un point du plan fait partie ou non de l’ensemble de Mandelbrot, nous allons pouvoir visualiser cet ensemble en utilisant l’outil informatique. L’algorithme est le suivant :

Affecter à MAX_ITERATION une valeur seuil
Pour chaque pixel C de coordonnées (x;y) de l'écran
    Convertir (x;y) dans le système de coordonnées du repère
    Tant Que la distance OMn < 2 et que n < MAX_ITERATION
        Calculer les coordonnées de Mn
        Affecter à n la valeur n+1
    Fin Tant Que
    Si n = MAX_ITERATION Alors
        Colorier le pixel en noir
    Sinon
        Colorier le pixel en blanc
    Fin Si
Fin Pour

L’algorithme est relativement simple. Il balaye l’écran pixel par pixel en convertissant ses coordonnées dans le système de coordonnées de notre repère pour savoir si celui-ci fait partie ou non de l’ensemble de Mandelbrot. A la sortie de la boucle « Tant Que », deux cas de figures se présentent :

• Soit on est sorti de la boucle parce que la distance \( OM_n \) est devenue plus grande que 2 auquel cas le pixel (et donc le point \( C \)) ne fait pas partie de l’ensemble de Mandelbrot, on lui attribue alors la couleur blanche.
• Soit on est sorti de la boucle parce que le seuil du nombre d’itérations maximales est atteint, c’est-à-dire qu’on a calculé suffisamment de termes de la suite pour considérer que la distance \( OM_n \) restera toujours plus petite que 2 auquel cas le pixel (et donc le point \( C \)) fait partie de l’ensemble de Mandelbrot et on lui attribue la couleur noire.

Ce qui donne en Python :

# Programme : mandelbrot.py
# Langage : Python 3.6 - Pygame 1.9
# Auteur : Mathieu
# Description : Calcule et affiche la fractale de Mandelbrot en noir et blanc

import pygame

# Constantes
MAX_ITERATION = 50 # nombre d'itérations maximales avant de considérer que la suite converge
XMIN, XMAX, YMIN, YMAX = -2, +0.5, -1.25, +1.25 # bornes du repère
LARGEUR, HAUTEUR = 500, 500 # taille de la fenêtre en pixels

# Initialisation et création d'une fenêtre aux dimensions spécifiéés munie d'un titre
pygame.init()
screen = pygame.display.set_mode((LARGEUR,HAUTEUR))
pygame.display.set_caption("Fractale de Mandelbrot")


# Création de l'ensemble de Mandelbrot
# Principe : on balaye l'écran pixel par pixel en convertissant le pixel en un point du plan de notre repère
# Si la suite converge, le point appartient à l'ensemble de Mandelbrot et on colore le pixel en noir
# Sinon la suite diverge, le point n'appartient pas à l'ensemble et on colore le pixel en blanc

for y in range(HAUTEUR):
  for x in range(LARGEUR):
    # Les deux lignes suivantes permettent d'associer à chaque pixel de l'écran de coordonnées (x;y)
    # un point C du plan de coordonnées (cx;cy) dans le repère défini par XMIN:XMAX et YMIN:YMAX
    cx = (x * (XMAX - XMIN) / LARGEUR + XMIN)
    cy = (y * (YMIN - YMAX) / HAUTEUR + YMAX)
    xn = 0
    yn = 0
    n = 0
    while (xn * xn + yn * yn) < 4 and n < MAX_ITERATION: # on teste que le carré de la distance est inférieur à 4 -> permet d'économiser un calcul de racine carrée coûteux en terme de performances
      # Calcul des coordonnes de Mn
      tmp_x = xn
      tmp_y = yn
      xn = tmp_x * tmp_x - tmp_y * tmp_y + cx
      yn = 2 * tmp_x * tmp_y + cy
      n = n + 1
    if n == MAX_ITERATION:
      screen.set_at((x, y), (0, 0, 0)) # On colore le pixel en noir -> code RGB : (0,0,0)
    else:
      screen.set_at((x, y), (255, 255, 255)) # On colore le pixel en blanc -> code RGB : (255,255,255)
pygame.display.flip() # Mise à jour et rafraîchissement de la fenêtre graphique pour affichage

# Boucle infinie permettant d'afficher à l'écran la fenêtre graphique
# Sans ça, la fenêtre apparaît et disparaît aussitôt
loop = True
while loop:
  for event in pygame.event.get():
    if event.type == pygame.QUIT: # Pour quitter l'application en fermant la fenêtre
      loop = False
      
pygame.quit()

Quelques précisions sur ce programme s’imposent. Il fonctionne sous Python 3.6 et utilise la librairie PyGame en version 1.9 que l’on peut télécharger à cette adresse. Celle-ci permet d’accéder aux ressources graphiques du système afin de manipuler une image au niveau du pixel et elle est relativement facile d’utilisation lorsqu’on se limite à des programmes simples. Sache tout de même, que cette bibliothèque graphique est très puissante et qu’elle permet par ailleurs de créer des jeux vidéos en Python d’où son nom 😉 .

Et voici enfin le moment de visualiser l’ensemble de Mandelbrot :

III – La fractale de Mandelbrot en couleurs

La visualisation précédente permet de saisir la structure fondamentale de l’ensemble de Mandelbrot. Toutefois, la visualisation en couleur va permettre de générer de belles images très esthétiques. L’idée est de colorer le pixel en fonction du rang à partir duquel la suite diverge. Plus ce rang est petit, plus la suite diverge rapidement et plus le pixel sera sombre. En revanche, plus ce rang est grand, plus la suite a mis « longtemps » à diverger et plus le pixel sera clair. On va ainsi faire apparaître des dégradés de couleurs aux frontières de l’ensemble de Mandelbrot. Pour cela, rien de bien compliqué, il te suffit de remplacer la ligne 43 par celle-ci :

screen.set_at((x, y), ((3 * n) % 256, (1 * n) % 256, (10 * n) % 256))

Le code RGB pour attribuer une couleur à un pixel est composé de trois nombres compris entre 0 et 255 qui représentent respectivement la quantité de rouge, de vert et de bleu.  Le calcul de N modulo 256, ici par exemple \( (3\times n)\% 256 \) renvoie le reste de la division euclidienne de N par 256, c’est-à-dire un nombre entre 0 et 255, ce qui va permettre justement de « doser » la quantité de chaque couleur fondamentale. Pour visualiser l’ensemble avec d’autres nuances de couleur, il te suffit de modifier le coefficient multiplicateur de \( n \) pour chaque couleur. Avec les coefficients ci-dessus, voici la belle fractale que l’on obtient :

IV – Plongée dans la fractale de Mandelbrot

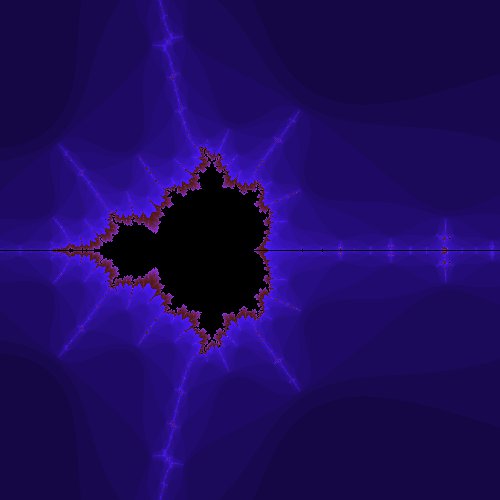
En observant de plus près l’ensemble de Mandelbrot, on peut déceler la propriété d’auto-similarité d’une fractale. En effet, sur l’axe de symétrie vers la gauche de l’image, on peut distinguer un motif qui semble rappeler l’ensemble en lui-même. Nous allons pour le vérifier faire un zoom sur cette zone. Pour cela, il faut modifier dans le programme précédent les bornes du repère en remplaçant la ligne 10 par celle-ci :

XMIN, XMAX, YMIN, YMAX = -1.8, -1.7, -0.05, 0.05

Vous devriez désormais voir apparaître cette image qui confirme bien que dans cette zone, on retrouve un motif qui ressemble fortement au motif initial :

Il est même possible de trouver des copies conformes de l’ensemble de Mandelbrot dans l’ensemble lui-même. Pour faciliter la recherche des zones où zoomer, nous allons rajouter quelques lignes de codes qui vont permettre d’afficher les coordonnées du point où l’utilisateur clique avec la souris. Pour cela, remplace la boucle d’affichage de la fenêtre par le code suivant :

while loop:
  for event in pygame.event.get():
    if event.type == pygame.QUIT: # Pour quitter l'application en fermant la fenêtre
      loop = False
    elif event.type == pygame.MOUSEBUTTONDOWN:
      p = pygame.mouse.get_pos()
      px = (p[0] * (XMAX - XMIN) / LARGEUR + XMIN)
      py = (p[1] * (YMIN - YMAX) / HAUTEUR + YMAX)
      print("({};{})".format(px,py))

Désormais, ton programme « surveille » les clics de la souris, récupère les coordonnées du pixel cliqué, les convertit dans le repère utilisé et les affiche. Il ne reste plus qu’à modifier les bornes du repère mais veille bien à garder une fenêtre carrée afin de ne pas déformer la figure. Amuse-toi à faire varier les couleurs, à zoomer sur des zones qui te semblent intéressantes et n’hésite pas à modifier le programme afin de l’adapter à tes propres besoins.

V- Pour aller plus loin

Il existe des logiciels qui permettent de voyager dans l’univers des fractales et qui vont générer de magnifiques images grâce à de très jolis dégradés de couleurs. Certains peuvent même générer des fractales en trois dimensions. Rendez-vous sur Wikipédia à la rubrique « Logiciels générateurs de fractales » en fin de page pour en savoir plus.

Il existe bien d’autres structures fractales. Parmi elles, l’une des plus célèbres est la fractale de Julia dont la définition récurrente est la suivante :

\( \left\lbrace\begin{array}{l} x_0=x_{\text{pixel}}\qquad y_0=y_{\text{pixel}}\\ x_{n+1}=x_n^2-y_n^2 +c_x\\ y_{n+1}= 2x_ny_n+c_y\end{array}\right. \)

Cette fois-ci, on balaye l’écran en affectant à \( x_0 \) et à \( y_0 \) les coordonnées du pixel dont on souhaite savoir s’il fait partie ou non de l’ensemble. \( c_x  \) et \( c_y \) représentent maintenant des paramètres fixés qui servent de « graine » à la génération de l’ensemble de Julia. On obtient donc avec ce procédé une infinité d’ensemble de Julia paramétré par les valeurs de \( c_x  \) et de \( c_y  \). Tu peux modifier le programme en le testant avec les paramètres suivants : \( c_x = 0,285 \) et \( c_y = 0,01  \). En remplaçant les lignes 28 à 31 par les lignes suivantes :

xn = (x * (XMAX - XMIN) / LARGEUR + XMIN)
yn = (y * (YMIN - YMAX) / HAUTEUR + YMAX)
cx = 0.285
cy = 0.01

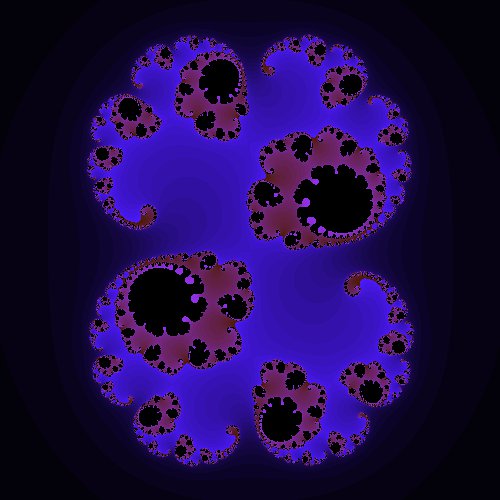
et en remplaçant les bornes du repère par celle-ci :

XMIN, XMAX, YMIN, YMAX = -1.25, 1.25, -1.25, +1.25

tu devrais obtenir la jolie fractale ci-dessous :

On peut également « jouer » avec la formule de récurrence afin d’obtenir des fractales dérivées de l’ensemble de Mandelbrot mais il faudra pour cela en passer par l’utilisation des nombres complexes. Si tu es en terminale S, tu peux t’y frotter et modifier le programme en conséquence pour les utiliser. Voici alors la suite complexe à itérer :

\( \left\lbrace\begin{array}{l} z_0=0\\ z_{n+1}=z_n^2 +c\end{array}\right. \)

Où \( c \) est l’affixe du point pour lequel on désire savoir s’il appartient ou non à l’ensemble de Mandelbrot et le calcul de la distance \( OM_n \) étant remplacé par le calcul du module de \( z_n \).

Enfin, la beauté des fractales vient surtout de l’algorithme de coloration utilisé. Tu trouveras sur internet des algorithmes beaucoup plus complexes que celui utilisé dans cet article, notamment ceux basés sur l’utilisation des logarithmes qui permettent de « lisser » le dégradé de couleurs.

On ne peut que s’émerveiller devant l’immense complexité des « paysages » obtenus en rapport de l’étonnante simplicité des formules qui les génèrent. Ce qui contribue encore davantage au charme de ces objets mathématiques bien mystérieux.

Pour conclure, il faut également savoir qu’il existe en économie une théorie établie par Benoît Mandelbrot lui-même et dans laquelle il propose une approche fractale des marchés financiers considérant que le cours d’une action en bourse possède cette fameuse propriété d’auto-similarité. Ainsi, si l’on observe la courbe des variations d’une action boursière sur une grande échelle de temps, on remarque qu’à des échelles plus petites, on peut retrouver le même motif de variations. Mais pour plus d’informations à ce sujet, il faudra s’en remettre à la lecture de son livre dans lequel il développe cette théorie.