Dans cet article, nous allons détailler les calculs qui permettent d’établir la formule de remboursement d’un emprunt bancaire. On donnera également les programmes Python, TI et Casio pour avoir toujours sous la main ce petit outil indispensable. Ces calculs font intervenir les suites et s’adressent plutôt à des élèves de première ou de terminale S et ES.
I – Un exemple concret d’emprunt bancaire
Imagine qu’un ami te demande de lui prêter 1200€. Comme c’est un très bon ami et que tu n’as pas de problème d’argent, tu acceptes volontiers de lui rendre ce petit service et comme c’est un ami honnête, il te propose de te les rembourser en 12 mois soit 100€ par mois.
Imagine maintenant que tu souhaites te faire un peu d’argent sur son dos (bon c’est pas très sympa mais imaginons quand même). Pour cela, tu va lui demander de te rembourser ces 1200€ au taux d’intérêt de \( 12\% \) annuel soit \( 1\% \) mensuel c’est-à-dire que tous les mois, \( 1\% \) de la somme qu’il lui reste à te donner ira directement dans ta poche. Tu lui demandes aussi de te verser tous les mois la somme de 90€ jusqu’à ce qu’il ait fini de te rembourser les 1200€. Ton ami accepte mais la question qu’il se pose alors est la suivante : pendant combien de mois devrai-je payer ?
Au départ, le capital restant dû est de 1200€. Pour calculer le capital restant dû le moi suivant, on augmente le capital précédent de \( 1\% \) correspondant au taux d’intérêt mensuel soit \( 1200+1200\times\frac{1}{100} = 1212 \) euros, montant duquel on va déduire la mensualité de remboursement de 90€ soit \( 1212 – 90 = 1122 \) euros. Il reste donc à payer au bout d’un mois 1122€. On recommence le même calcul pour calculer ce qu’il reste à rembourser au bout de deux mois et ainsi de suite. Un tableur permet de visualiser rapidement ce qu’il reste à payer chaque mois. On construit avec ce type d’outil (Microsoft Excel, LibreOffice Calc ou encore Apple Numbers) ce qu’on appelle le tableau d’amortissement du prêt :
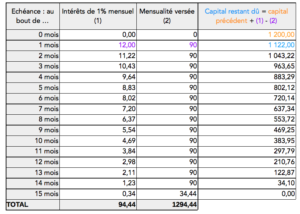
Ton ami t’a remboursé 90€ pendant 14 mois et une dernière mensualité ajustée de 34€44 pour solder le prêt soit un montant total d’intérêts de \( 14\times 90 +34,44 -1200 = 94,44 \) euros.
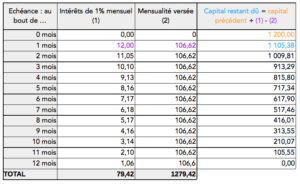
Si ton ami veut à tout prix rembourser son crédit en 12 mois, la problématique devient alors la suivante : quelle est la somme constante à verser chaque mois pour solder le prêt en exactement 12 mois. Réponse : 106€62 avec une dernière mensualité légèrement ajustée à cause des arrondis effectués.
II – Le cas général
La banque prête un capital de \( C \) € au taux annuel de \( T\% \) sur une durée de \( N \) mois. On cherche la somme constante notée \( M \) à verser mensuellement pour solder le prêt en exactement \( N \) mois. On note également :
- \( t \) le taux mensuel en pourcentage, donc \( t = \frac{T}{12} \)
- \( C_N \) le capital restant dû à la banque le \( N^\text{ième} \) mois, donc \( C_0 = C \)
Le capital restant dû le \( (N+1)^\text{ième} \) mois s’obtient alors ainsi :
\(\begin{array}{rl}C_{N+1} = & C_N + \frac{t}{100}\times C_N – M\\ = & (1+\frac{t}{100})C_N – M\\ = & qC_n-M \end{array} \)
On définit ainsi une suite arithmético-géométrique pour laquelle on pose \( q = 1+\frac{t}{100} \) afin de rendre plus lisible les calculs qui vont suivre. Il reste alors à rembourser :
- au bout d’1 mois :
\( C_1 = qC_0 – M \)
- au bout de 2 mois :
\( \begin{array}{rl} C_2 = & qC_1 – M \\= & q(qC_0 – M)-M\\ =& q^2C_0-qM-M \end{array} \)
- au bout de 3 mois :
\( \begin{array}{rl} C_3 = & qC_2 – M \\= & q(q^2C_0-qM-M)-M\\ =& q^3C_0-q^2M-qM-M \end{array} \)
- au bout de \( N \) mois, on démontre grâce à un raisonnement par récurrence (tu peux essayer si tu es en TS) que \( C_N \) s’écrit sous la forme :
\( \begin{array}{rl} C_N = & q^NC_0-M-qM-q^2M-\ldots -q^{N-1}M\\ = & q^NC_0-M(1+q^2+\ldots +q^{N-1})\end{array} \)
Le terme \(1+q^2+\ldots +q^{N-1} \) est la somme des \( N \) termes d’une suite géométrique de raison \( q \) et de premier terme 1 pour laquelle on dispose d’une formule (voir ton cours de terminale sur les suites). Ainsi, \(1+q^2+\ldots +q^{N-1} = 1\times \frac{1-q^N}{1-q} \) et il vient alors :
\( C_N = q^NC_0-M\times \frac{1-q^N}{1-q}\)
On cherche alors à exprimer la mensualité \( M \) permettant de solder le prêt le \( N^{\text{ième}} \) mois c’est-à-dire telle que \( C_N = 0 \) .
\( \begin{array}{rl} C_N = 0 \iff & q^NC_0-M\times \frac{1-q^N}{1-q} = 0 \\ \iff & M\times \frac{1-q^N}{1-q} = q^NC_0 \\ \iff & M = q^NC_0\times \frac{1-q}{1-q^N}\end{array} \)
On peut aussi chercher à évaluer sa capacité d’emprunt connaissant sa capacité de remboursement mensuelle et la durée du prêt. Cela revient à isoler \( C_0 \) dans l’équation précédente :
\( \begin{array}{rl} C_N = 0 \iff & q^NC_0-M\times \frac{1-q^N}{1-q} = 0 \\ \iff & q^NC_0 = M\times \frac{1-q^N}{1-q} \\ \iff & C_0 = M\times \frac{1-q^N}{q^N(1-q)} \end{array} \)
III – Codage et tests
Suivant le matériel dont tu disposes, voici les différents programmes à taper :
En Python 3
"""
Programme : emprunt.py
Langage : Python 3
Auteur : Matt
Description : calcule la mensualité ou la capacité d'emprunt d'un prêt bancaire
"""
print("Que voulez-vous faire ?")
print("1 - Calculer mes mensualités")
print("2 - Calculer ma capacité d'emprunt")
choix = int(input("Votre choix : "))
if (choix == 1) :
C = float(input("Capital emprunté en euros : "))
T = float(input("Taux annuel en % : "))
N = int(input("Durée en mois : "))
t = T / 12 # calcul du taux mensuel
q = 1 + t / 100 # calcul du coefficient multiplicateur associé à une hausse de t%
M = q**N * C * (1 - q) / (1 - q**N)
print("Votre mensualité sera de {0:.2f} euros".format(M))
I = N * M - C # calcul des intérêts versés
print("Le montant total des intérêts versés sera de {0:.2f} euros".format(I))
elif (choix == 2) :
M = float(input("Capacité de remboursement mensuelle en euros : "))
T = float(input("Taux annuel en % : "))
N = int(input("Durée en mois : "))
t = T / 12
q = 1 + t / 100
C = M * (1 - q**N) / (q**N * (1 - q))
print("Votre capacité d'emprunt s'élève à {0:.2f} euros".format(C))
I = N * M - C
print("Le montant total des intérêts versés sera de {0:.2f} euros".format(I))
Pour calculatrice CASIO

Pour calculatrice Ti

Pour calculatrice Ti-Nspire

Afin de vérifier que ton programme fonctionne correctement, voici les résultats qu’il doit t’afficher :
- Pour un emprunt de 10000€ à \( 4\% \) annuel sur 36 mois, la mensualité s’élève à 295,24€
- Pour un prêt au taux de \( 3\% \) annuel remboursable en 240 mensualités de 500€, la capacité d’emprunt est de 90155,46€
Voilà, tu disposes maintenant d’un outil bien pratique qui te permettra plus tard de discuter d’égal à égal avec ton banquier. Et pour les plus téméraires d’entre vous ou pour ceux qui souhaitent s’orienter vers des études en informatique, pourquoi ne pas tenter de le programmer sur ton téléphone en y installant les outils de développement Android ou Apple ?

